QuickSort is a sorting algorithm based on the Divide and Conquer algorithm that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array.
How does QuickSort work?
The key process in quickSort is a partition(). The target of partitions is to place the pivot (any element can be chosen to be a pivot) at its correct position in the sorted array and put all smaller elements to the left of the pivot, and all greater elements to the right of the pivot.
Partition is done recursively on each side of the pivot after the pivot is placed in its correct position and this finally sorts the array.
How Quicksort works
Choice of Pivot:
There are many different choices for picking pivots.
Partition Algorithm:
The logic is simple, we start from the leftmost element and keep track of the index of smaller (or equal) elements as i. While traversing, if we find a smaller element, we swap the current element with arr[i]. Otherwise, we ignore the current element.
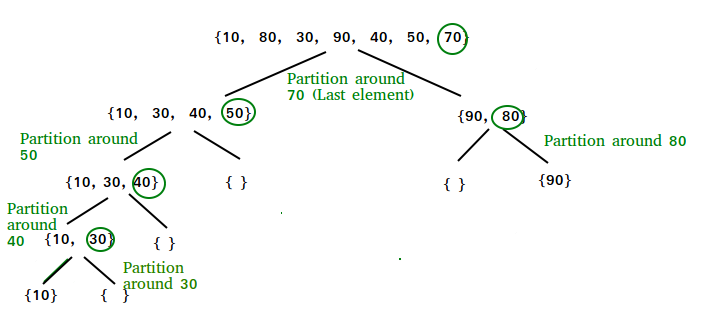
Let us understand the working of partition and the Quick Sort algorithm with the help of the following example:
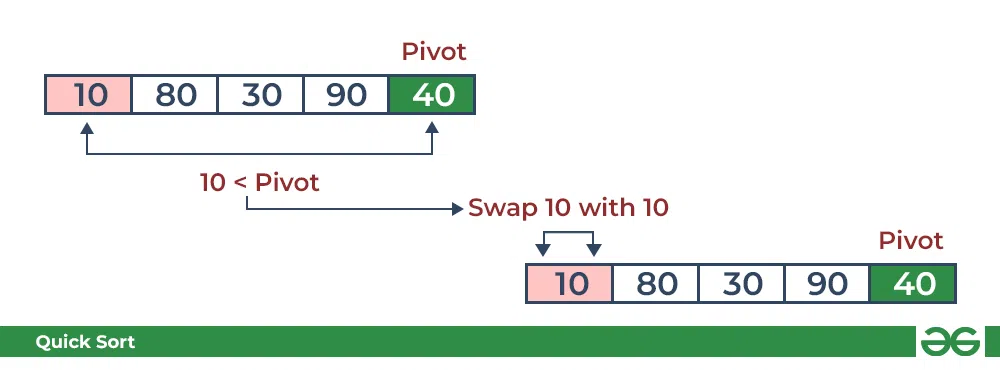
Consider: arr[] = {10, 80, 30, 90, 40}.
- Compare 10 with the pivot and as it is less than pivot arrange it accrodingly.
Partition in QuickSort: Compare pivot with 10
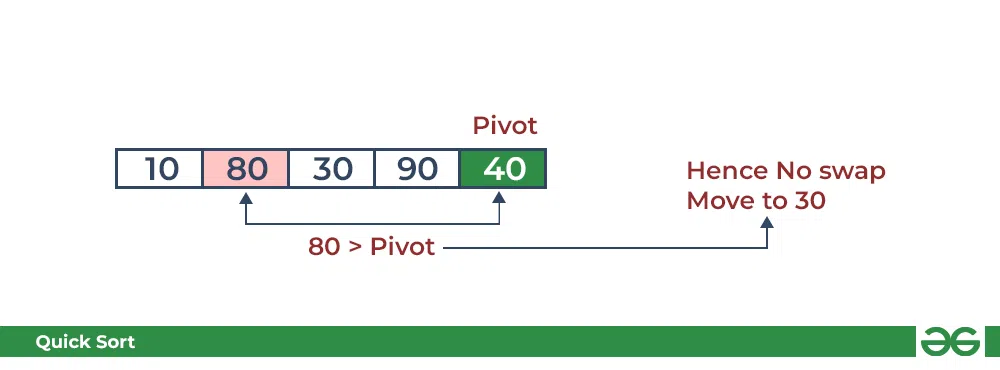
- Compare 80 with the pivot. It is greater than pivot.
Partition in QuickSort: Compare pivot with 80
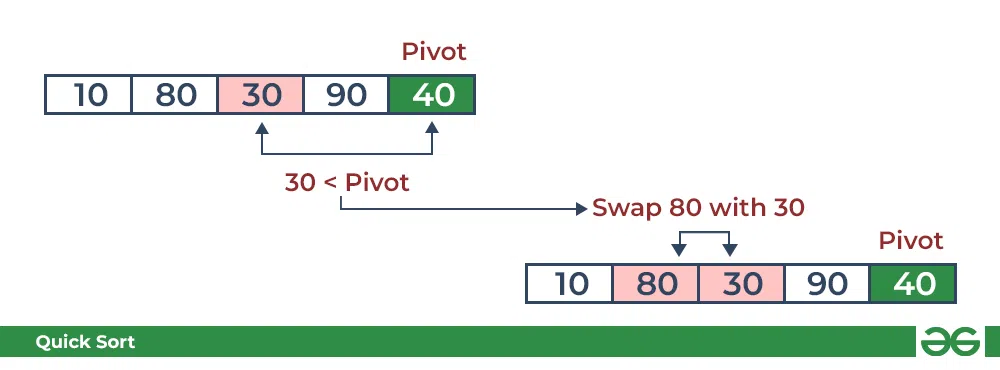
- Compare 30 with pivot. It is less than pivot so arrange it accordingly.
Partition in QuickSort: Compare pivot with 30
- Compare 90 with the pivot. It is greater than the pivot.
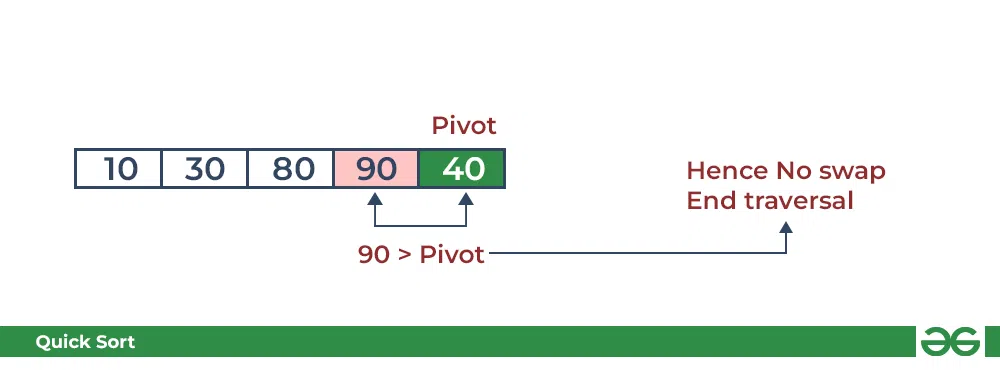
Partition in QuickSort: Compare pivot with 90
- Arrange the pivot in its correct position.
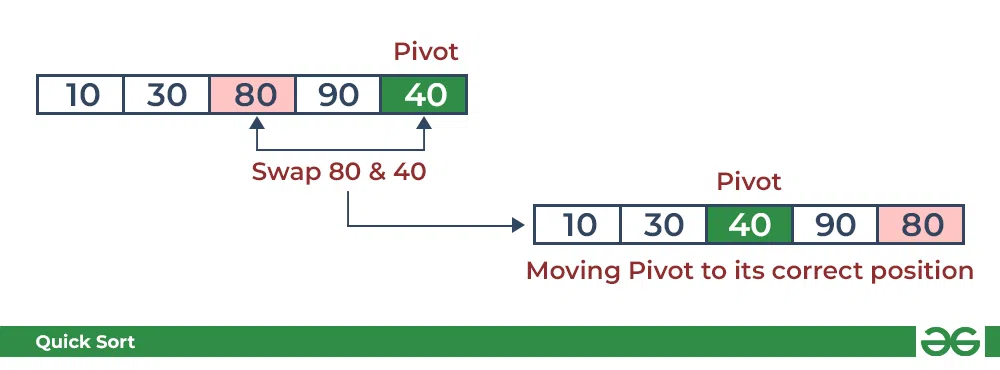
Partition in QuickSort: Place pivot in its correct position
Illustration of Quicksort:
As the partition process is done recursively, it keeps on putting the pivot in its actual position in the sorted array. Repeatedly putting pivots in their actual position makes the array sorted.
Follow the below images to understand how the recursive implementation of the partition algorithm helps to sort the array.
- Initial partition on the main array:
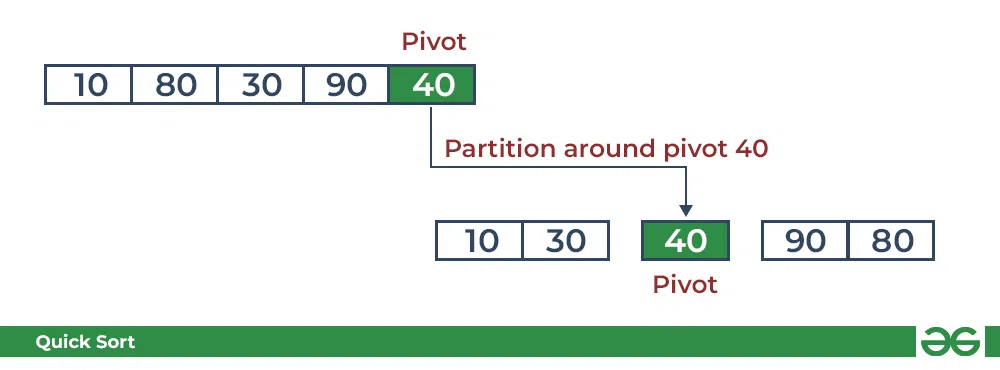
Quicksort: Performing the partition
- Partitioning of the subarrays:

Quicksort: Performing the partition
Code implementation of the Quick Sort:
C++
#include <bits/stdc++.h>
using namespace std;
int partition(int arr[],int low,int high)
{
int pivot=arr[high];
int i=(low-1);
for(int j=low;j<=high;j++)
{
if(arr[j]<pivot)
{
i++;
swap(arr[i],arr[j]);
}
}
swap(arr[i+1],arr[high]);
return (i+1);
}
void quickSort(int arr[],int low,int high)
{
if(low<high)
{
int pi=partition(arr,low,high);
quickSort(arr,low,pi-1);
quickSort(arr,pi+1,high);
}
}
int main() {
int arr[]={10,7,8,9,1,5};
int n=sizeof(arr)/sizeof(arr[0]);
quickSort(arr,0,n-1);
cout<<"Sorted Array\n";
for(int i=0;i<n;i++)
{
cout<<arr[i]<<" ";
}
return 0;
}
|
Java
import java.io.*;
class GFG {
static void swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static int partition(int[] arr, int low, int high)
{
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return (i + 1);
}
static void quickSort(int[] arr, int low, int high)
{
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
public static void printArr(int[] arr)
{
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
public static void main(String[] args)
{
int[] arr = { 10, 7, 8, 9, 1, 5 };
int N = arr.length;
quickSort(arr, 0, N - 1);
System.out.println("Sorted array:");
printArr(arr);
}
}
|
Python3
def partition(array, low, high):
pivot = array[high]
i = low - 1
for j in range(low, high):
if array[j] <= pivot:
i = i + 1
(array[i], array[j]) = (array[j], array[i])
(array[i + 1], array[high]) = (array[high], array[i + 1])
return i + 1
def quicksort(array, low, high):
if low < high:
pi = partition(array, low, high)
quicksort(array, low, pi - 1)
quicksort(array, pi + 1, high)
if __name__ == '__main__':
array = [10, 7, 8, 9, 1, 5]
N = len(array)
quicksort(array, 0, N - 1)
print('Sorted array:')
for x in array:
print(x, end=" ")
|
C#
using System;
class GFG {
static void swap(int[] arr, int i, int j)
{
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
static int partition(int[] arr, int low, int high)
{
int pivot = arr[high];
int i = (low - 1);
for (int j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j);
}
}
swap(arr, i + 1, high);
return (i + 1);
}
static void quickSort(int[] arr, int low, int high)
{
if (low < high) {
int pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
public static void Main()
{
int[] arr = { 10, 7, 8, 9, 1, 5 };
int N = arr.Length;
quickSort(arr, 0, N - 1);
Console.WriteLine("Sorted array:");
for (int i = 0; i < N; i++)
Console.Write(arr[i] + " ");
}
}
|
Javascript
function partition(arr, low, high) {
let pivot = arr[high];
let i = low - 1;
for (let j = low; j <= high - 1; j++) {
if (arr[j] < pivot) {
i++;
[arr[i], arr[j]] = [arr[j], arr[i]];
}
}
[arr[i + 1], arr[high]] = [arr[high], arr[i + 1]];
return i + 1;
}
function quickSort(arr, low, high) {
if (low < high) {
let pi = partition(arr, low, high);
quickSort(arr, low, pi - 1);
quickSort(arr, pi + 1, high);
}
}
let arr = [10, 7, 8, 9, 1, 5];
let N = arr.length;
quickSort(arr, 0, N - 1);
console.log("Sorted array:");
console.log(arr.join(" "));
|
PHP
<?php
function partition(&$arr,$low,$high)
{
$pivot= $arr[$high];
$i=($low-1);
for($j=$low;$j<=$high-1;$j++)
{
if($arr[$j]<$pivot)
{
$i++;
list($arr[$i],$arr[$j])=array($arr[$j],$arr[$i]);
}
}
list($arr[$i+1],$arr[$high])=array($arr[$high],$arr[$i+1]);
return ($i+1);
}
function quickSort(&$arr,$low,$high)
{
if($low<$high)
{
$pi= partition($arr,$low,$high);
quickSort($arr,$low,$pi-1);
quickSort($arr,$pi+1,$high);
}
}
$arr= array(10,7,8,9,1,5);
$N=count($arr);
quickSort($arr,0,$N-1);
echo "Sorted Array:\n";
for($i=0;$i<$N;$i++)
{
echo $arr[$i]. " ";
}
?>
|
Output
Sorted array:
1 5 7 8 9 10
Time Complexity:
- Best Case: Ω (N log (N))
The best-case scenario for quicksort occur when the pivot chosen at the each step divides the array into roughly equal halves.
In this case, the algorithm will make balanced partitions, leading to efficient Sorting.
- Average Case: θ ( N log (N))
Quicksort’s average-case performance is usually very good in practice, making it one of the fastest sorting Algorithm.
- Worst Case: O(N2)
The worst-case Scenario for Quicksort occur when the pivot at each step consistently results in highly unbalanced partitions. When the array is already sorted and the pivot is always chosen as the smallest or largest element. To mitigate the worst-case Scenario, various techniques are used such as choosing a good pivot (e.g., median of three) and using Randomized algorithm (Randomized Quicksort ) to shuffle the element before sorting.
- Auxiliary Space: O(1), if we don’t consider the recursive stack space. If we consider the recursive stack space then, in the worst case quicksort could make O(N).
Advantages of Quick Sort:
- It is a divide-and-conquer algorithm that makes it easier to solve problems.
- It is efficient on large data sets.
- It has a low overhead, as it only requires a small amount of memory to function.
Disadvantages of Quick Sort:
- It has a worst-case time complexity of O(N2), which occurs when the pivot is chosen poorly.
- It is not a good choice for small data sets.
- It is not a stable sort, meaning that if two elements have the same key, their relative order will not be preserved in the sorted output in case of quick sort, because here we are swapping elements according to the pivot’s position (without considering their original positions).
Feeling lost in the world of random DSA topics, wasting time without progress? It's time for a change! Join our DSA course, where we'll guide you on an exciting journey to master DSA efficiently and on schedule.
Ready to dive in? Explore our Free Demo Content and join our DSA course, trusted by over 100,000 geeks!