CBSE class 12 previous year’s question paper for the subject mathematics is the very essential tool in the arsenal of students preparing for the Class 12 board examination. It helps students to understand the pattern of the question paper of the board exam and also gave students an opportunity to evaluate their preparation before the examination. Students also got to know the proper way to write solutions for the examination as the solution of the paper is also provided.
By using CBSE Previous Year Paper for Mathematics students can gain more confidence in attempting the board examination and also they get to know about the lacking areas of their preparation. All the mistakes made during this mock examination can help students avoid making similar errors in the board examinations.
Section -A
(Very Short Answer Questions)(2×6=12)
Question 1: Find the sum of the order and the degree of the differential equation:
(x+dy/dx)2 = (dy/dx)2 +1
Answer:
Given differential equation,
(x+dy/dx)2 = (dy/dx)2 +1
on simplifying,
x2 + (dy/dx)2 + 2x(dy/dx) = (dy/dx)2 + 1
Subtracting (dy/dx)2 from both sides we get,
x2 + 2x(dy/dx) = 1
Now,
Order of the above Differential Equation is 1
Degree of the above Differential Equation is 2
So the sum is 1+1 = 2
Read More on Differential Equations
Question 2: In a Parallelogram PQRS, 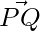 = 3i-2j+2k and
= 3i-2j+2k and 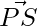 = -i-2k. Find the |QS| and |PR|.
= -i-2k. Find the |QS| and |PR|.
Answer:
Given,
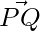 = 3i-2j+2k
= 3i-2j+2k
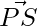 = -i-2k
= -i-2k
By triangular law of vector,
\vec{QS} = \vec{PS} – \vec{PQ}
= (-i-2k) – (3i-2j+2k)
=(-4i+2j-4k)
|QS| = (16+4+16)1/2 =(36)1/2=6.
Similarly,
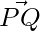 +
+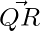 =
=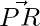
=>(3i-2j+2k)+(-i-2k)
=(2i-2j)
|PR|=(4+4)1/2= (8)1/2.
Also, Check Vector Operations
Question 3 a: If d(F(x))/dx = sec4x / cosec4x F(π/4)=π/4, then find F(x).
Answer:
If d/dx [F(x)] = sec4x/cosec4x
By taking integration both sides,
∫sec4x/cosec4x dx = F(x)
F(x) = ∫tan4xdx
∫tan²x (sec²x-1)dx [tan2x = sec2x – 1]
= ∫tan²xsec²dx – ∫tan²x dx
= ∫tan²xsec²xdx – ∫(sec²x -1) dx
By using Method of substitution:
let, tanx=t
Differentiating both sides with respect to x,
=>sec2x = dt/dx
=>sec2x dx= dt
Now, the equation is:
= ∫ t2dt – tanx + x+ c
= t3/3 – tanx + x + c
Now Putting the values into the equation:
F(x) = tan³x/3 – tan x + x+ c
=> F(π/4) = 1/3 – 1 + π/4 + c
=> π/4 = 1/3 – 1 + π/4 + c
=> xc = 1-1/3 = 2/3
F(x) = tan³x /3 – tan x + x + 2/3.
Read More on Differentiation
OR
Question 3 b: Find Integration of (logx -3) /(logx)4 .dx.
Answer:
∫ log x – 3/(log x)4 dx
By using Method of substitution:
logx = t
Differentiating both sides with respect to x,
1/x = dt/dx
dx= xdt [logx=t => x=et]
=>dx= etdt
Now putting the values into the equation:
∫ t-3/t4 (et dt)
= et(1/t3 – 3/t4)dt
= et/t3 + c
Putting the values into the equation:
= e logx/(logx)3 + c
= x/(log x)3 +c where, c=constant
Read More on Indefinite Integrals
Question 4: Let A and B be two events such that P(A)=5/8, P(B)=1/2, and P(A/B)= 3/4. Find the value of P(B/A).
Answer:
We know that,
P(B/A)= P(A.B)/P(A)
P(A/B)=P(A.B)/P(B)
=>P(A.B)= P(A/B) × P(B)
=3/4 × 1/2
=3/8
So, P(B/A) = (3/8) / (5/8)
=3/5.
Also Check, Probability Theory
Question 5: Two balls are drawn at random from a bag containing 2 red balls and 3 blue balls, without replacement. Let the variable X denote the number of red balls. Find the probability distribution of X.
Answer:
For X = No. of red balls is taken i.e., X = (BB),
P(X) = 3/5 × 2/4
= 6/20 = 3/10
For X = One Ball is red is taken i.e., X(BR, RB)
P(X) = 3/5 × 2/4 + 2/5 × 3/4
= 6/20 + 6/20 = 12/20 = 3/5
For X = Both Red Balls are taken i.e., X(RR)
P(X) = 2/5 × 1/4
= 2/20 = 1/10
| X |
0 |
1 |
2 |
| P(X) |
3/10 |
3/5 |
1/10 |
Question 6: Find the value of Lambda, for which the distance of Point(2,1, λ) from plane 3x+5y+4z=11 is 81/2 units.
Answer:
The distance from the pane to point is:
2√2 = 3(2) + 5(1) + 4(λ) -III/√9+25+16
= 2√2×5√2 = |6+5+4λ – II
|4λ| = 20
4λ = ± 20
λ = ±5
Also, Check Linear Equations in One Variable
Section B
(Short Answer Type Questions) (4×3 = 12 Marks)
Question 7 a: If a, b, c and d are four non-zero vectors such that a×b = c×d and a×c = 4b×d then show that a-2d is parallel to 2b-c where a is not equal to 2d and c is not equal to 2b
Answer:
If a vector is non-zero then it has at least one non-zero component, a zero vector has all components as 0’s therefore no length.
Consider the LHS and RHS of the given
It more or less equivalent to the commutative law,
a-2d is parallel to 2b-c where a is not equal to 2d and c is not equal to 2b,
Here, we consider the following equation so as to get the value,
Vectors when multiplied in scalar in 1 and when
multiplied using vector becomes zero
Here,
We take example,
A×A = 0
Following the procedure in the sum for same,
We get,
a x b-a x c = c x d-b x d
=> ax(b-c)=(c-b) x d
=> ax(b-c)-(c-b) x d=0
⇒ ax(b-c)-dx(b−c) = 0
(a-d)x(b-c)=0
⇒ (a-d) || (b-c)
(a-d) (b-c)+0
a.b+d.c is not equal to d.b+ a.c
Hence, the required answer is a.b+d.c is not equal to d.b+ a.c
OR
Question 7 b: The two adjacent sides of a parallelogram are 2i-4j-5k and 2i+2j+3k Find the unit vector parallel to its diagonal. Also, find the area of the parallelogram also.
Answer:
Let
X and Y are adjacent side of a parallelogram, where
X=2 i-4 j−5k and
Y= 2i+2 j+3k
Let diagonal be Z
Hence
Z= X+ Y=(2 i- 4 j−5k)+( 2i+2 j+3 k)=4 i-2 j-2 k
|Z|= 42 + 22 +22
= 16+4+4
=√24.
Unit vector in direction of Z = 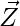 / |Z|
/ |Z|
=> (1/√24) ×(4i-2j-2k).
Area of Parallelogram= Modulus((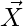 *
*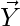 ) [cross product of X and Y]
) [cross product of X and Y]
= i(-12+10) +j(6+10) +k(4+8)
=-2i+16j+12k
Modulus = √4+256+144
=√404 Sq units
Also Check, Area of Parallelogram in Vector Form
Question 8: Find the vector equation of the plane passing through the intersection of the planes r.(2i+2j-3k)=7 and r.(2i+5j+3k)=9 and through the point (2,1,3).
Answer:
Let,
X1=2i+2j−3k
X2=2i+5j+3k
M1=7
M2=9
r.(X1+λX2)=M1+λM2
r[2i+2j−3k+λ(2j+5j+3k)]=7+λ9
r[i(2+2λ)+j(2+5λ)+k(−3+3λ)]=7+9λ
Taking r=xi+yj+zj
We get,
(2+2λ)x+(2+5λ)y+(−3+3λ)z=7+9λ
(2x+2y−3z−7)+λ(2x+5y+3z−9)=0
Given, it passes through (2,1,3)
(4+2−9−7)+λ(4+5+9−9)=0
λ= 10/9
Putting in above equation,
r.( 38/9i+ 68/9j +3/9k)=17
Question 9 a: Find Integration of dx/(x1/2 + x1/3).
Answer:
Let, I=∫ x 1/2+x 1/3dx
Taking L.C.M of denominator of
1/2 and 1/3
which is 6.
So x=t 6
⇒dx=6t5
Now
I=∫ 6t5/t 3+t 2 dt
=∫6t5/ t2(t+1)dt
=∫ 6t3/t+1dt
=∫ 6[(t3+1)-1]dt
=6∫(t2−t+1− 1/(t+1))dt
=6[t3/3 – t2/2 + t – log(t+1)] +C
=6[√x/3 – x1/3/ 2 + x1/6 – log(x1/6 +1)] +C
OR
Question 9 b: How do you evaluate the definite integral
∫cosx/(1+sinx)(4+sinx) from[0, π/2]?
Answer:
Given that,
∫π/2 cosx /(1+sinx)(4+sinx)dx
0
By Method of substitution:
Let, 1+sinx=t
cosx dx=dt.
=∫12 dt/t(3+t)
= 1/3 × ∫12 1/t – 1/(3+t) dt
=1/3 × [logt – log(3+ t)]12
=1/3 × [log2 -log (5) – (log1 – log4)]
=1/3 ×[log2 – log5 + log4]
Question 10: Find the particular solution of the differential equation
x dy/dx +x cos2(y/x) =y. Given that when x=1, y=π/2.
Answer:
Given that,
x dy/dx +x cos2(y/x) =y
=>dy/dx +cos2(y/x)= y/x
=>dy/dx = y/x – cos2(y/x)
BY using Method of substitution:
Let, y=ux
dy/dx=u+x × du/dx
Now, Substituting the value into our diff. eq.
u+ x × du/dx = ux/x – cos2(ux/x)
u+ x × du/dx = u – cos2(u)
x × du/dx=- cos2u
sec2u du= -dx/x
On Integrating both sides we get,
tanu =-logx+ C
tan(y/x) + logx = C
C= Log1
Hence, tan(y/x) +logx= log1
Section C
(4×4=16 Marks)
Question 11 a: Using Integration, Find the Area of the region: {(x, y): 4x2 +9y2 <=36, 2x+3y>=6}.
Answer:
Given Equations are:
4X2 + 9Y2 <=36 ……..(1)
divide by 36 both sides, we get
X2/9+ Y2/4=1
=>X2/32 +Y2/ 22 = 1
Comparing the above Equation with,
X2 / a2 + Y2 /b2 =1
We get,
a=3, b=2
And, 2X+3Y =6 ……..(2)
Pont of intersection is:
2X + 3Y =6
Squaring both sides, we get
(2X +3Y)2 = 36
4X 2+ 9Y2 + 6XY = 36
36+ 12 XY =36
12XY =0
X=0, Y=0
Now Putting these values in Eq (2), we get
Point P1(0,2) and P2(3,0).
Area of the region is :
=∫y1dx – ∫y2 dx [range is (0,3)]
=∫2/3 √(9-x2) dx – ∫ 2/3 × (3-x) dx
=2/3[ x/2 √(9-x2) – 9/2 × sin-1x/3]- (3x-x2/2 ) ]
=2/3 × 9/2 × π/2 – 2/3 × 9/2
= 3/2 ×π – 3 square units
OR
Question 11 b: Using integration, find the area of the region bounded by the line y − 1 = x, the x-axis, and x = −2 and x = 3.
Answer:
We have Equations,
x-y = -1 ….. ( 1 )
x = -2 …… ( 2 )
x = 3 ….. ( 3 )
Equation (1) represents a straight line intersecting x−axis at (−1,0) and y−axis at (0,1).
Equation (2) represents a straight line parallel to y−axis at a distance of 2 units on the left of y−axis.
Equation (3) represents a straight line parallel to y−axis at a distance of 3 units on the right of y−axis.
Points of intersection:
put x=−2 in (1), we get y=−1
put x=3 in (1), we get y=4
Let AB be the given line, intersecting the x−axis at C(−1,0).
Required area = Area CDAC+ Area CBEC
=∫ydx +∫ (−y)dx
=∫ (x+1)dx+∫ −(x+1)dx
= [ x2/2+x]-13 (range: 3 to -1) −[ x2 /2+x] (range : -1 to -2)
= [( 9/2+3)−( 1/2−1)]−[( 1/2−1)−(2−2)]
= 15/2+ 1/2+ 1/2
= 17/2
= 8.5 square unit
Read More on Area Under The Curve
Question 12: A card from a pack of 52 cards is lost from the remaining cards of the pack, two cards are drawn at random(without Replacement) and are found to be both Aces. Find the probability of the lost card being an ace.
Answer:
Let E1 be the event that the lost card is Aces.
Given that there are 4 Aces in the deck P(E1)= 4/52= 1/13
Let E2 be the even that the lost card is not a Ace P(E2) = 1 – P(E1) = 1- 1/13 = 12/13
Let A be the event that the two cards drawn are both Aces,
P(A/E1)= No. of ways of drawing 2 Aces cards/ Total no .of ways of drawing 2 cards
= 3C2/ 51C2
= 3/51 × 2/50
P(A/E2) = 4C2 / 51C2 = 4/51 × 3/50
Applying Bayes Theorem, where
P(E1/A) = [P(E1) × P(A/E1)] / [P(E1) × P(A/E1) + P(E2) × P(A/E2)]
= [1/13 × 3/51 × 2/50] / [ 1/13 × 3/51 × 2/50 + 12/13 × 4/51 × 3/50
= 6/150
= 1/25
Question 13: Evaluate: ∫0π x/(1+sinx)dx
Answer:
Let I=∫ x/(1+sinx)dx …….(1)
⇒ I=∫ (π−x)/(1+sin(π−x))dx, (∵∫f(x)dx=∫f(a−x)dx)
⇒I=∫ (π−x)/ (1+sinx) dx …………. (2)
Adding (1) and (2), we obtain
2I=∫ π/ (1+sinx)dx
⇒ 2I=π∫ (1−sinx)/(1+sinx)(1−sinx)dx
⇒ 2I = π∫ (1−sinx)/(1-sin2x)dx
⇒ 2I=π∫ (1−sinx)/cos2xdx [1-sin2x= cos2x]
⇒ 2I = π∫ (1/cos2x – sinx/cos2x) dx
⇒ 2I=π∫ {sec2x−tanxsecx}dx
⇒ 2I = π[tanx−secx]0π
⇒ 2I = π[1+1]= 2π
⇒ I=π
Question 14: Electrical transmission wires which are laid down in winter are stretched tightly to accommodate expansion in summer
Two such wires lie along the following lines.
I1 : (x + 1)/3 = (y-3)/-2 = (z+2)/-1
I2 = x/-1 = (y-7)/3 = (z + 7)/-2
Based on the given information, answer the following questions:
(i) Are the lines I1 and I2 coplanar? Justify your answer.
(ii) Find the point of intersection of lines I1 and I2.
Answer:
Given,
I1 : (x + 1)/3 = (y-3)/-2 = (z+2)/-1
I2 = x/-1 = (y-7)/3 = (z + 7)/-2
(i)
| x2 -x1 = a1, a2
y2 – y1 = b1, b2
z2– z1 = c1, c2 |
(a2 – a1). (b1×b2) = 0
(ii)
-3λ + 1 = +µ
-2λ + 3 = 3µ + 7
-2λ + 3 = 9λ +3 + 7
7λ = 7
λ = 1
(α, β, γ) = (2, 1, -3)
For further assistance read,
Whether you're preparing for your first job interview or aiming to upskill in this ever-evolving tech landscape,
GeeksforGeeks Courses are your key to success. We provide top-quality content at affordable prices, all geared towards accelerating your growth in a time-bound manner. Join the millions we've already empowered, and we're here to do the same for you. Don't miss out -
check it out now!