Set Theory is a branch of Mathematics that studies the collection of objects and operations based on it. Sets are studied under the mathematical logic division of mathematics. A set is simply a collection of objects. The words collection, aggregate, and class are synonymous. On the other hand element, members, and objects are synonymous and stand for the members of the set of which the set is comprised. In this article on Set Theory, we will learn about sets, types of sets, representation of sets, operations on sets, and application of sets in detail.
History of Set Theory
The concept of Set Theory was propounded in the year 1874 by Georg Cantor in his paper name ‘On a Property of Collection of All Real Algebraic Numbers’. His concept of Set Theory was later used by other mathematicians in giving various other theories such as Klein’s Encyclopedia and Russell Paradox. Sets Theory is a foundation for a better understanding of topology, abstract algebra, and discrete mathematics.
Sets Definition
Sets are defined as ”a well-defined collection of objects”. Let’s say we have a set of Natural Numbers then it will have all the natural numbers as its member and the collection of the numbers is well defined that they are natural numbers. A set is always denoted by a capital letter. For Example, a set of Natural Numbers is given by N = {1, 2, 3, 4…..}. The term ‘well defined’ should be taken care of, as if we try to make a set of best players, then the term ‘best’ is not well defined. The concept of best, worst, beautiful, powerful, etc. varies according to the notions, assumptions, likes, dislikes, and biases of a person.
Elements of a Set
The objects contained by a set are called the elements of the set. For Example, in the set of Natural Numbers 1, 2, 3, etc are the objects contained by the set, hence they are called the elements of the set of Natural Numbers. We can also say that 1 belongs to set N. It is represented as 1 ∈ N, where ∈ is the symbol of belongs to.
Cardinal Number of a Set
The number of elements present in a set is called the Cardinal Number of a Set. For Example, let’s say P is a set of the first five prime numbers given by P = {2, 3, 5, 7, 11}, then the Cardinal Number of set P is 5. The Cardinal Number of Set P is represented by n(P) or |P| = 5.
Example of Sets
A Set is a well-defined collection of objects. The objects inside a set are called members of the set. Some examples of sets are mentioned below:
Set of Natural Numbers: N = {1, 2, 3, 4….}
Set of Even Numbers: E = {2, 4, 6, 8…}
Set of Prime Numbers: P = {2, 3, 5, 7,….}
Set of Integers: Z = {…, -4, -3, -2, -1, 0, 1, 2,….}
Some Standard Sets used in Set Theory
- Set of Natural Numbers is denoted by N
- Set of Whole Numbers is denoted by W
- Set of Integers is denoted by Z
- Set of Rational Numbers is denoted by Q
- Set of Irrational Numbers is denoted by P
- Set of Real Numbers is denoted by R
Representation of Sets
Sets are primarily represented in two forms
- Roster Form
- Set Builder Form
Roster Form
In the Roster Form of the set, the elements are placed inside braces {} and are separated by commas. Let’s say we have a set of the first five prime numbers then it will be represented by P = {2, 3, 5, 7, 11}. Here the set P is an example of a finite set as the number of elements is finite, however, we can come across a set that has infinite elements then in that case the roster form is represented in the manner that some elements are placed followed by dots to represent infinity inside the braces. Let’s say we have to represent a set of Natural Numbers in Roster Form then its Roster Form is given as N = {1, 2, 3, 4…..}.
Set Builder Form
In Set Builder Form, a rule or a statement describing the common characteristics of all the elements is written instead of writing the elements directly inside the braces. For Example, a set of all the prime numbers less than or equal to 10 is given as P = {p : p is a prime number ≤ 10}. In another example, the set of Natural Numbers in set builder form is given as N = {n : n is a natural number}.
Read More on Representation of Sets
Types of Sets
There are different types of sets categorized on various parameters. The different types of sets are explained below:
Empty Set
A set that has no elements inside it is called an Empty Set. It is represented by Φ or {}. For Example A = {x : x ∈ N and 2 < x < 3}. Here, between 2 and 3, no natural number exists, hence A is an Empty Set. Empty Sets are also known as Null Sets.
Singleton Set
A set that has only one element inside it is called a Singleton Set. For Example, B = {x : x ∈ N and 2 < x < 4} = {3}. Here between 2 and 3 only one element exists, hence B is called a Singleton Set.
Finite Set
A set that has a fixed or finite number of elements inside it is called a Finite Set. For Example A = {x : x is an even number less than 10} then A = {2, 4, 6, 8}. Here A has 4 elements, hence A is a finite set. The number of elements present in a finite set is called the Cardinal Number of a finite set. It is given as n(A) = 4.
Infinite Set
A set that has an indefinite or infinite number of elements inside it is called a Finite Set. For Example A = {x : x is an even number l} then A = {2, 4, 6, 8……}. Here A has unlimited elements, hence A is an infinite set.
Equivalent Sets
If the number of elements present in two sets is equal i.e. the cardinal number of two finite sets is the same then they are called Equivalent Sets. For Example, A = {x : x is an even number up to 10} = {2, 4, 6, 8, 10} and B = {y : y is an odd number less than 10} = {1, 3, 5, 7, 9}. Here, the cardinal number of set A is n(A) = 5 and that of B is given as n(B) = 5 then we see that n(A) = n(B). Hence A and B are equivalent sets.
Equal Sets
If the number of elements and also the elements of two sets are the same irrespective of the order then the two sets are called equal sets. For Example, if set A = {2, 4, 6, 8} and B ={8, 4, 6, 2} then we see that number of elements in both sets A and B is 4 i.e. same and the elements are also the same although the order is different. Hence, A and B are Equal Sets. Equal Sets are represented as A = B.
Unequal Sets
If at least any one element of one set differs from the elements of another set then the two sets are said to be unequal sets. For Example, if set A = {2, 4, 6, 8} and B = {4, 6, 8, 10} then set A and B are unequal sets as 2 is present in set A but not in B and 10 is present in set B but not in A. Hence, one element differs between them thus making them unequal. However, the cardinal number is the same therefore they are equivalent sets.
Overlapping Sets
If at least any one element of the two sets are the same then the two sets are said to be overlapping sets. For Example, if set A = {1, 2, 3} and set B = {3, 4, 5} then we see that 3 is the common element between set A and set B hence, set A and set B are Overlapping Sets.
Disjoint Sets
If none of the elements between two sets are common then they are called the Disjoint Sets i.e., for two sets A and B if A. For Example, set A = {1, 2, 3} and set B = {4, 5, 6} then we observe that there is no common element between set A and set B hence, set A and B are Disjoint Sets.
Apart from the above-mentioned sets, there are other sets called, Subsets, Supersets, Universal Sets, and Power Sets. We will learn them below in detail.
Read, Types of Sets
Subsets
If A and B are two sets such that every element of set A is present in set B then A is called the subset of B. It is represented as A ⊆ B and read as ‘A is a subset of B’. Mathematically it is expressed as
A ⊆ B iff
a ∈ A ⇒ a ∈ B
If A is not a subset of B we write it as A ⊄ B.
For Example, if A = {1, 2} and B = {1, 2, 3} then we see that all the elements of A are present in B, hence A ⊆ B. There are two kinds of subset Proper Subset and Improper Subset.
Proper Subset
If a subset doesn’t contain all the elements of the set or has fewer elements than the original set then it is called the proper subset. For example, in set A = {1, 2} and B = {1, 2, 3}, the subset A doesn’t contain all the elements of the original set B, hence A is a proper subset of B. It is represented as A ⊂ B. Empty set is a proper subset of a given set as it has no elements.
Improper Subset
If a subset contains all the elements that are present in the original set then it is called an Improper Subset. For Example, if set A = {1, 2, 3, 4} and set B = {1, 2, 3, 4} then A is the improper subset of set B. It is mathematically expressed as A ⊆ B. Thus we deduce that two sets are equal iff A ⊆ B and B ⊆ A. It should be noted that an empty set is an improper subset of itself.
Some Important Results on Subset
- Every set is a subset of itself
- An empty Set is a subset of every set.
- The number of possible subsets for a given finite set with ‘n’ number of elements is equal to 2n.
- N ⊂ W ⊂ Z ⊂ Q ⊂ R and T ⊂ R where N is a set of Natural Numbers, W is a set of Whole Numbers, Z is a set of integers, Q is a set of Rational Numbers, T is a set of irrational numbers and R is set of real numbers.
Superset
If all the elements of set A are present in set B then set B is called the Superset of set A. It is represented as B ⊇ A. Let’s say if A = {2, 3, 4} and B = {1, 2, 3, 4} then we see that all elements of set A are present in set B, hence B ⊇ A. If a superset has more elements than its subset then it is called a proper or strict superset. A Proper Superset is represented as B ⊃ A. Some of the Properties of Supersets are mentioned below:
- Every set is a superset of itself.
- Every set is a superset of an empty set.
- Total number of possible supersets for a given subset is infinite
- If B is a superset of A then A is a subset of B
Universal Set
The set that contains all the sets in it is called a Universal Set. Let’s say set A = {1, 2, 3}, set B = {4, 5}, and set C = {6, 7} then Universal Set is given as U = {1, 2, 3, 4, 5, 6, 7}. Another Example of a Universal Set is U = {Set of All Living Beings} then which includes both floras and faunas. Flora and fauna are the subsets of Universal Sets U.
Power Set
A set that contains all the subsets as its element is called the Power Set. For Example, if set A = {1, 3, 5} then its subsets are {Φ}, {1}, {2}, {3}, {1, 3}, {3, 5}, {1, 5} and {1, 3, 5} then its Power Set is given as P(A) = {{Φ}, {1}, {2}, {3}, {1, 3}, {3, 5}, {1, 5}, {1, 3, 5}}. As we know the number of possible subsets for a finite set containing n elements is given by 2n then the number of elements in the power set is also 2n
Set Theory Symbols
There are various symbols that are used in Sets Theory. The symbol and their explanation are tabulated below:
| {} |
Set |
| x ∈ A |
x is an element of set A |
| x ∉ A |
x is not an element of set A |
| ∃ or ∄ |
There exist or there doesn’t exist |
| Φ |
Empty Set |
| A = B |
Equal Sets |
| n(A) |
Cardinal Number of Set A |
| P(A) |
Power Set |
| A ⊆ B |
A is a subset of B |
| A ⊂ B |
A is the Proper subset of B |
| A ⊈ B |
A is not a subset of B |
| B ⊇ A |
B is the superset of A |
| B ⊃ A |
B is a proper superset of A |
| B ⊉ A |
B is not a superset of A |
| A ∪ B |
A union B |
| A ∩ B |
A intersection B |
| A’ |
Complement of Set A |
Learn More, Set Symbols
Sets Operation
The sets undergo various operation which includes their union of sets, the intersection of sets, the difference of sets, the complement of sets, and the Cartesian Product of Sets. We will learn them briefly below:
Union of Sets
Union of Sets basically refers to uniting two sets and writing their elements in a single set without repeating elements if common elements are present. The union of sets is given by A ∪ B.
For Example if Set A = {2, 4} and Set B = {4, 6} then A ∪ B = {2, 4} ∪ {4, 6} = {2, 4, 6}
Intersection of Sets
Intersection of sets refers to finding the common elements between two sets. It is given by A ∩ B. For Example if set A = {2, 4} and B = {4, 6} then A ∩ B = {2, 4} ∩ {4, 6} = {4}.
Difference of Sets
Difference of Sets refers to the deletion of common elements of two sets and writing down the remaining elements of two sets. It is represented as A – B. For Example if et A = {2, 4} and B = {4, 6} then A – B = {2, 6}
Complement of Set
Compliment of Set refers to the set of elements from the universal set excluding the elements of the set of which we are finding the compliment. It is given by A’. For Example, if we have to find out the complement of the set of Natural Numbers then it will include all the numbers in the set from the Real Numbers except the Natural Numbers. Here Real Number is the Universal set of Natural Numbers.
Cartesian Product of Sets
Cartesian Product of Sets refers to the product between the elements of two sets in ordered pair. It is given as A ✕ B. For Example if set A = {2, 4} and B = {4, 6} then A ✕ B = {(2,4), (2,6), (4,4), (4,6)}.
Learn More, Operation on Sets
The set theory formulas are given for two kinds of sets overlapping and disjoint sets. Let’s learn them separately
Given that two sets A and B are overlapping, the formulas are as follows:
| n(A ∪ B) |
n(A) + n(B) – n(A ∩ B) |
| n(A ∩ B) |
n(A) + n(B) – n(A ∪ B) |
| n(A) |
n(A ∪ B) + n(A ∩ B) – n(B) |
| n(B) |
n(A ∪ B) + n(A ∩ B) – n(A) |
| n(A – B) |
n(A ∪ B) – n(B) |
| n(A – B) |
n(A) – n(A ∩ B) |
| n(A ∪ B ∪ C) |
n(A) + n(B) + n(C) – n(A∩B) – n(B∩C) – n(C∩A) + n(A∩B∩C) |
If two sets A and B are disjoint sets
| n(A ∪ B) |
n(A) + n(B) |
| (A ∩ B) |
Φ |
| n(A – B) |
n(A) |
Properties of Sets
The various properties followed by sets are tabulated below:
| Commutative Property |
A ∪ B = B ∪ A
A ∩ B = B ∩ A
|
| Associative Property |
(A ∩ B) ∩ C = A ∩ (B ∩ C)
(A ∪ B) ∪ C = A ∪ (B ∪ C)
|
| Distributive Property |
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
|
| Identity Property |
A ∪ Φ = A
A ∩ U = A
|
| Complement Property |
A ∪ A’ = A |
| Idempotent Property |
A ∪ A = AA ∩ A = A |
De Morgan’s Law
De Morgan’s Law is applicable in relating the union and intersection of two sets via their complements. There are two laws under De Morgan’s Law. Let’s learn them briefly
De Morgan’s Law of Union
De Morgan’s Law of Union states that the complement of the union of two sets is equal to the intersection of the complement of individual sets. Mathematically it can be expressed as
(A ∪ B)’ = A’ ∩ B’
De Morgan’s Law of Intersection
De Morgan’s Law of Intersection states that the complement of the intersection of two sets is equal to the union of the complement of individual sets. Mathematically it can be expressed as
(A ∩ B)’ = A’ ∪ B’
Venn Diagram
Venn Diagram is a technique for representing the relation between two sets with the help of circles, generally intersecting. For Example, two circles intersecting with each other with the common area merged into them represent the union of sets, and two intersecting circles with a common area highlighted represents the intersection of sets while two circles separated from each other represents the two disjoint sets. A rectangular box surrounding the circle represents the universal set. The Venn diagrams for various operations of sets are listed below:
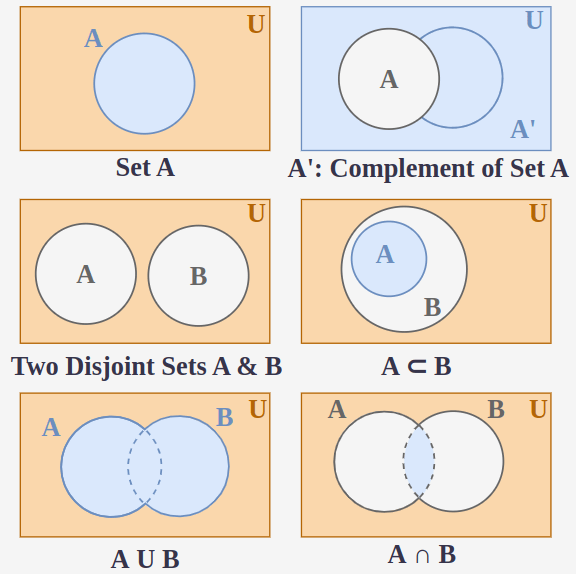
Also, Read
Solved Examples on Set Theory
Example 1: If A and B are two sets such that n(A) = 17 and n(B) = 23 and n(A ∪ B) = 38 then find n(A ∩ B).
Solution:
We know that n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
⇒ 38 = 17 + 23 – n(A ∩ B)
⇒ n(A ∩ B) = 40 – 38 = 2
Example 2: If X = {1, 2, 3, 4, 5}, Y = {4, 5, 6, 7, 8}, and Z = {7, 8, 9, 10, 11}, find (X ∪ Y), (X ∪ Z), (Y ∪ Z), (X ∪ Y ∪ Z), and X ∩ (Y ∪ Z)
Solution:
(X ∪ Y) = {1, 2, 3, 4, 5} ∪ {4, 5, 6, 7, 8} = {1, 2, 3, 4, 5, 6, 7, 8}
(X ∪ Z) = {1, 2, 3, 4, 5} ∪ {7, 8, 9, 10, 11} = {1, 2, 3, 4, 5, 7, 8, 9, 10, 11}
(Y ∪ Z) = {4, 5, 6, 7, 8} ∪ {7, 8, 9, 10, 11} = {4, 5, 6, 7, 8, 9, 10, 11}
(X ∪ Y ∪ Z) = {1, 2, 3, 4, 5} ∪ {4, 5, 6, 7, 8} ∪ {7, 8, 9, 10, 11} = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11}
X ∩ (Y ∪ Z) = {1, 2, 3, 4, 5} ∩ {4, 5, 6, 7, 8, 9, 10, 11} = {4, 5}
FAQs on Set Theory
1. What is Set Theory?
Set Theory is the study of a collection of objects which are called sets and the relation between different sets.
2. Define Sets
Sets are a well-defined collection of objects. These objects are called the element of sets.
3. Who Invented Set Theory?
Set Theory was invented by German Mathematician Georg Cantor.
4. What is Algebra of Sets?
Algebra of Sets deals with the following laws:
- Commutative Laws
- Associative Law
- Distributive Law
- Identity Law
- Idempotent Law
These laws are covered in the article under Properties of Sets.
5. What is a Subset?
A subset is a set that has fewer or equal elements of another set. The other set is called a Superset.
6. What is De Morgan’s Law?
De Morgan’s Law is a law that deals with the union and intersection of sets with the intersection and union of individual sets respectively. There are two laws under it namely De Morgan’s Law of Union and De Morgan’s Law of Intersection. These are covered under the section of De Morgan’s Law in this article.
Whether you're preparing for your first job interview or aiming to upskill in this ever-evolving tech landscape,
GeeksforGeeks Courses are your key to success. We provide top-quality content at affordable prices, all geared towards accelerating your growth in a time-bound manner. Join the millions we've already empowered, and we're here to do the same for you. Don't miss out -
check it out now!