Linear Algebra

Linear Algebra is one of the key mathematical disciplines that work with vectors, matrices, and linear equations. It is the most widely used mathematical concept all around the world. There are several disciplines which include physics, engineering, computer science, economics, and others that use Linear Algebra as a key tool. The primary focus of linear Algebra is on linear transformations which are functions that map one vector space to another while maintaining the vector space’s structure. Matrix, which are rectangular arrays of integers, may be used to depict these transformations. 

Table of Contents

• Definition
• Linear Algebra Branches
• Vectors
• Linear Function
• Linear Matrix
• Numerical Linear Algebra
• Applications of Linear Algebra
• Solved Examples
• FAQs

What is Linear Algebra?

The Branch of Mathematics which deals with matrices, vectors, finite and Infinite spaces is called Linear Algebra. It is used in various fields including applied mathematics, physics, and engineering. Linear Algebra is the study of vector spaces, linear equations, linear functions, and matrices.

The general linear equation is represented as u₁x₁ + u₂x₂+…..u_nx_n= v

Here,

• u’s – represents the coefficients
• x’s – represents the unknowns
• v – represents the constant

There is a collection of equations called a System of linear algebraic equations. It obeys the linear function such as –

 (x₁,……..x_n) → u₁x₁+……….+u_nx_n

Linear Algebra Branches

Linear Algebra is divided into different branches based on the difficulty level of topics that come under linear algebra – Elementary Linear Algebra, Advanced, and Applied Linear Algebra.

Elementary Linear Algebra

Elementary Linear algebra generally covers the topic of basic linear algebra such as Scalars and Vectors, Matrix and matrix operation, etc.

Scalars: Those physical quantities that have a magnitude and size only but don’t have direction in them are called scalar quantities. Scalars are the real numbers in linear algebra. Scalars are used to check that a variable such as a is just a real number and not a vector or matrix.

Vector: Those quantities that have both magnitude and direction are called vector quantities. They play a crucial role in linear algebra and are the elements of a vector space. They are usually denoted using an arrow above the quantity, and they possess both direction and magnitude. Vectors operations like addition and scalar multiplication are essential concepts in linear algebra. Matrices are a collection of vectors arranged in a rectangular array.

Vector Space: It is linear space a group of objects called vectors, added collectively and multiplied(scaled )by numbers, called scalars.

Matrix: A rectangular array of integers organized in rows and columns in linear algebra. The letters a, b, c, and other similar letters are commonly used to represent the integers that make up a matrix’s entries is called Matrix.

Advance Linear Algebra

Advanced linear algebra mostly covered all the advanced topics related to linear algebra such as Linear function, Linear transformation, Eigenvectors, and Eigenvalues, etc.

Linear Transformation: Linear transformations are functions that preserve linear relationships between vectors, and they are vital in solving systems of linear equations. A linear function which is also known as linear transformation is an essential tool in linear algebra, providing a systematic approach to understanding and manipulating linear relations between vectors. 

Eigenvectors and Eigenvalues: In general Eigenvectors and eigenvalues are applied during linear transformation when the eigenvectors of a matrix A is a vector represented by a matrix X such that when X is multiplied with matrix A, then the direction of the resultant matrix remains the same as vector X.  AX = λX where A is any arbitrary matrix, λ are eigenvalues and X is an eigenvector corresponding to each eigenvalue.

The inverse of a Matrix: The Inverse of the Matrix is denoted by A^-1 and When we multiply the inverse of a matrix with a given matrix then we will get multiplicative identity. Thus, A. A^-1 = A^-1A = I, where I is the identity matrix.

Applied Linear Algebra 

In applied linear algebra there are topics covered are generally the practical implications of Elementary and advanced linear Algebra topics such as the Complement of a matrix, matrix factorization and norm of vectors, etc.

Vectors

Vectors play an important role in linear algebra and are the elements of vector space. They are usually shown as arrows in the elements, and they possess both direction and magnitude. Vectors operations like addition and scalar multiplication are mainly used concepts in linear algebra. They can be used to solve systems of linear equations and represent linear transformation, and perform matrix operations such as multiplication and inverse matrices.

The representation of many physical processes’ magnitude and direction using vectors, a fundamental component of linear algebra, is essential. In linear algebra, vectors are elements of a vector space that can be scaled and added. Essentially, they are arrows with a length and direction. The length of a vector is referred to as its magnitude, while the direction is the line that the vector points along.

Vector Space in Linear Algebra

It is a linear space a group of objects called vectors, added collectively and multiplied(scaled )by numbers, called scalars.

To add vectors, we add the corresponding components of each vector. Due to this, the sum of two vectors can be presented as  

a=(a₁+a₂+a₃) and b=(b₁+b₂+b₃)  a+b =(a₁+b₁, a₂+b₂, a₃+b₃).

A vector and a scalar, which is just an integer, are multiplied in scalar multiplication. For example, if we multiply a vector v by scaler c. we get a new vector cv whose magnitude is c times the magnitude of v, and whose direction is either the same or opposite.

For Example, If we want to subtract two vectors by using Linear Algebra we can take two vectors:

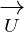 = (4,5,1) and  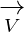= (6,1,7) 

when we subtract this we get

  
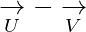 = ( -2,4,-6)

So the Final answer is = (-2,4,-6)

• Position and Displacement Vectors
• Vector Operations
• Product of Vectors | Scalar Product of Vectors
• How to calculate the Unit Vector?
• The angle between Two Vectors Formula
• Vector Projection Formula

Linear Function

A mathematical function known as a “linear function” also known as “Linear Transformation” in linear algebra retains the linear relationships between the vectors as it translates them from one vector space to another.

A linear function is characterized by two important properties. Firstly, it is addictive which means that the function preserves vector addition. Secondly, it is homogeneous, meaning the function preserves scalar multiplication.

A formal definition of a linear function is provided below:

f(ax) = af(x), and f(x + y) = f(x) + f(y)

where a is a scalar, f(x) and f(y) are vectors in the range of f, and x and y are vectors in the domain of f.

A function is a type of function that maintains the properties of vector addition and scalar multiplication when mapping between two vector spaces. Specifically a function T: V ->W is considered linear if it satisfies two key properties:

• Additive property : T(u+v)=T(u)+T(v)

for all vectors u and v in vector space V

• Homogeneous Property : T(cu)=cT(u)

for all vectors u in vector space V and scalars c

Basically, V and W refer to two vector spaces and the operation of vector addition and scalar multiplication define within each space. The additional property requires that the function T preserves the vector addition operation, meaning that the image of the sum of two vectors is equal to the sum of two images of each individual vector.

For example, we have a linear transformation T that takes a two-dimensional vector (x, y) as input and outputs a new two-dimensional vector (u, v) according to the following rule:

T(x, y) = (2x + y, 3x – 4y)

To verify that T is a linear transformation, we need to show that it satisfies two properties:

• Additivity: T(u + v) = T(u) + T(v)
• Homogeneity: T(cu) = cT(u)

Let’s take two input vectors (x1, y1) and (x2, y2) and compute their images under T:

T(x1, y1) = (2×1 + y1, 3×1 – 4y1) T(x2, y2) = (2×2 + y2, 3×2 – 4y2)

Now let’s compute the image of their sum:

T(x1 + x2, y1 + y2) = (2(x1 + x2) + (y1 + y2), 3(x1 + x2) – 4(y1 + y2)) = (2×1 + y1 + 2×2 + y2, 3×1 + 3×2 – 4y1 – 4y2) = (2×1 + y1, 3×1 – 4y1) + (2×2 + y2, 3×2 – 4y2) = T(x1, y1) + T(x2, y2)

So T satisfies the additivity property.

Now let’s check the homogeneity property. Let c be a scalar and (x, y) be a vector:

T(cx, cy) = (2(cx) + cy, 3(cx) – 4(cy)) = (c(2x) + c(y), c(3x) – c(4y)) = c(2x + y, 3x – 4y) = cT(x, y)

So T also satisfies the homogeneity property. Therefore, T is a linear transformation.

Overall the linear function is an essential tool in linear algebra, providing a systematic approach to understanding and manipulating linear relations between vectors. 

• Linear Equations in One Variable
• Linear Equations in Two Variables
• Simultaneous Linear Equations
• Solving Linear Equations
• Solutions of a Linear Equation
• Graphing Linear Equations
• Linear Dependence and Independence 

Linear Matrix

A matrix is a rectangular array of integers organized in rows and columns in linear algebra. The letters a, b, c, and other similar letters are commonly used to represent the integers that make up a matrix’s entries. Matrices are often used to represent linear transformation, such as scaling, rotation, and reflection.

A matrix’s size is determined by the rows and columns that are present. A matrix has three rows and two columns, for instance. A matrix is referred to as be 3×2 matrix, for instance, if it contains three rows and two columns. Matrix basically works on operations including addition, subtraction, and multiplication.

The appropriate elements are simply added or removed when matrices are added or subtracted. Scalar multiplication involves multiplying every entry in the matrix by a scalar(a number). Matrix multiplication is a more complex operation that involves multiplying and adding certain entries in the matrices.

The number of columns and rows in the matrix determines its size. For instance, a matrix with 4 rows and 2 columns is known as a 4×2 matrix. The entries in the matrix are integers, and they are frequently represented by letters like u, v, and w.

For example: Let’s consider a simple example to understand more, suppose we have two vectors, v₁, and v₂ in a two-dimensional space. We can represent these vectors as a column matrix, such as :

v₁ =   ,  v₂ =

Now we will apply a linear transformation that doubles the value of the first component and subtracts the value of the second component. Now we can represent this transformation as a 2×2 linear matrix A

A =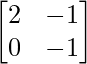 

To apply this to vector v₁, simply multiply the matrix A with vector v₁

Av₁ =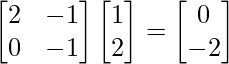 

 The resulting vector, [0,-2] is the transformed version of v₁. Similarly, we can apply the same transformation to v₂

Av₂ =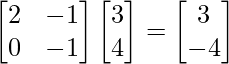 

The resulting vector, [3,-4] is the transformed version of v₂.

Numerical Linear Algebra

The development of numerical algorithms for solving linear equations and associated issues is the subject of numerical linear algebra, a branch of linear algebra. It entails using various matrix operations, linear transformations, and other principles to solve numerical problems.

It involves using different matrix operations, linear transformation, and other concepts to solve numerical problems.

One of the most popular uses of numerical linear algebra is to sort out a problem of linear equations. Another important area of linear algebra is eigenvalue and eigenvectors computation in a range of applications such as in physics, engineering, and computer graphics.

In numerical linear Algebra, there are various methods for computing eigenvalues and eigenvectors, such as the power method, QR algorithm, and Lanczos algorithm. The important part of numerical linear algebra is the linear equation

For example: Let us consider the given equations that are –

3x + 3y + 4z =20

5x + 6y + 7z = 30

8x + 9y + 10z = 40

 To solve this we use, 

AX = B

where A = coefficient matrix, X is the matrix of unknown variable, and b is the right-hand-side vector.

A =`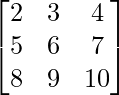    X =     b = 

Using matrix operation, we can solve for x by finding the inverse of A.

X = A^-1B

where A^{-1 i}s the inverse of A

Singular Value Decomposition(SVD) 

It is another concept in numerical linear algebra that plays an important role in data analysis and, machine learning. SVD  can be used for dimensionality reduction, noise reduction, and data compression.

It also includes applications in optimization, signal processing, and computer vision. In optimization, linear programming is a commonly used technique that involves solving a linear objective function subject to linear constraints. Signal processing applications include filtering and noise reduction, while computer vision applications involve image processing and recognition.

• Rank approximation
• Non-Negative Matrix Factorization

Applications of Linear Algebra

Linear Algebra is a fascinating branch of mathematics that deals with equations, transformations, and spaces. Several different problems that would be impossible to address without the usage of linear algebra may be resolved by applying its principles. We can resolve many complex problems by using Linear Algebra.

Linear algebra is a fascinating field that finds widespread use in computer graphics. The usage of linear algebra is essential for creating aesthetically attractive 3D models and compelling special effects in the worlds of movies and video games. Its engagement is critical in increasing the media’s overall appeal.

Machine learning is another field where linear algebra is used to build algorithms such as regression, classification, and clustering. This can help us to analyze and understand large amounts of data by making it easy to locate their trends and patterns. 

In Robotics, we utilize linear algebra to map and position robots, and it can even assist regulate robot moments. It’s incredible how it can allow us to operate robots remotely and simply grasp the quantum realm.

Optimization of problems is another area where linear algebra can be amazingly useful. It helps us to resolve complex problems by representing them mathematically and it helps to find optimal solutions to particular problems.

Overall, linear algebra is a strong tool that everybody interested in science and technology should study because it is useful in many domains such as machine learning and robotics. For resolving difficult issues that might otherwise be intractable. We can solve a wide range of complex issues using Linear Algebra Equations. Because of its adaptability, we can tackle a wide range of difficult problems. 

Practice Problems with Solution

Solved Examples on Linear Algebra

Example 1: Find the sum of the two vectors
= 2i + 3j + 5k and
= -i + 2j + k

Solution:

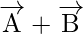= (2-1)i + (2 + 3)j + (5 + 1)k = i + 5j + 6k

Example 2: Find the dot product of
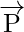= -2i + j + 3k and
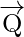= i – 2j + k

Solution:

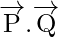= -2i(i – 2j + k) + j(i – 2j + k) + 3k(i – 2j + k)

= -2i -2j + 3k

Example 3: Find the solution of x + 2y = 3 and 3x + y = 5

Solution:

From x + 2y = 3 we get x = 3 – 2y

Putting this value of x in the second equation we get

3(3 – 2y) + y = 5

⇒ 9 – 6y + y = 5

⇒ 9 – 5y = 5

⇒ -5y = -4

⇒ y = 4/5

Putting this value of y in 1st equation we get

x + 2(4/5) = 3

⇒ x = 3 – 8/5

⇒ x = 7/5

Example 4: Find the sum of the two matrices
and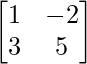

Solution:

Let the two matrices be P =
and Q = and S is also a 2 x 2 matrix given by P + Q

S = P + Q = + =

Example 5: Find the difference between two vectors 6i – 3j + 2k and 3i + 2j – 4k

Solution:

Let
= 6i – 3j + 2k and
= 3i + 2j – 4k

then = (6i – 3j + 2k ) – (3i + 2j – 4k) = 3i – 5j + 6k.

FAQs on Linear Algebra

Q1: Where is linear Algebra used in real life?

Answer: 

Linear algebra plays an important role to determine unknown quantities. Linear Algebra basically used for calculating speed, Distance, or Time and It is also used for projecting a three-dimensional view into a two-dimensional plane, handled by linear maps. It is also used to create ranking algorithms for search engines such as Google.

Q2: What are the 4 types of matrices?

Answer: 

There are basic four types of matrices are 

• Horizontal Matrix – [a_ij]_mxn where ,n > m
• Vertical Matrix – [a_ij]_mxn where, m > n
• Square Matrix – [a_ij]_mxn where, m = n
• Diagonal Matrix – A = [a_ij] when ,i ≠ j

Q3: What are Linear Algebra topics?

Answer: 

The most important topics covered in linear algebra include

• Eigenvectors and Egienvalues
• Orthogonal Matrices
• Linear Functions
• Matrix with mathematical operation 
• Linear Transformation
• Sparse Matrices

Q4: What is linear algebra in mathematics?

Answer: 

Linear algebra is a mathematical area which studies linear equations and their characteristics. 
Linear algebra is mainly focused on comprehending how various systems of linear equations behave and may be solved. This is performed by storing the equations in matrices and vectors, both of which are mathematical objects that may be handled in a number of ways.

Q5: What is a linear transformation matrix?

Answer: 

A linear transformation matrix is a general representation of a linear transformation between vector spaces. A linear transformation is a type of functioning in which there are properties of addition and scalar multiplication. it’s commonly used in fields such as physics, engineering, computer graphics and Machine learning. Linear matrix iworks as a significant tool in mathematics and its applications enables us to instantly do computations on vectors and other mathematical structures, and it has several practical applications in a variety of disciplines.